Incorporating higher-order interactions: extending network models to simplicial complexes
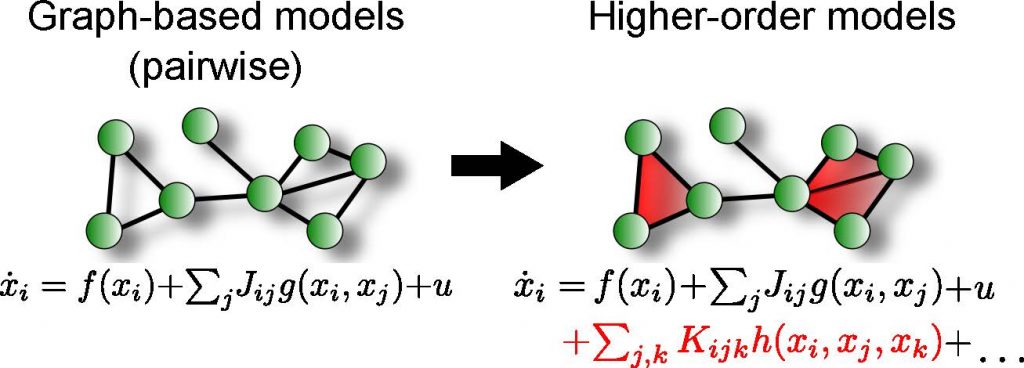
Graph-based models have enjoyed a tremendous success for modelling complex systems and networks over the past decades, however, fundamental interactions in networks often take place between multiple nodes.
Indeed, concurrent dynamical dependencies between multiple nodes, although typically neglected, are present in many systems. Consider for instance socio-economic networks, where group-based interactions are commonplace, often involving the joint coordinated activity of multiple agents (e.g. buyer, seller, broker). The importance of non-binary (so called supra-dyadic) interactions has also been long debated in the social sciences. For instance, structural balance theory implies that triadic relations in social networks will evolve according to the colloquial rules “the friend of a friend is my friend” and “the enemy of my enemy is my friend.”
In all these examples, the joint coordinated interplay between multiple entities is crucial, and cannot be captured naturally with a simple pairwise (binary) interaction model (Figures 1a-b). As graphs are fundamentally focusing on pairwise interactions (edges denote interactions between pairs of nodes), graph based models may therefore be insufficient to represent faithfully the dynamics of the system. In this context, simplicial complexes (SCs) provide an appropriate formalism that can integrate higher-order interactions into network models and extend graph-based models. SCs are finite collections of simplices (nodes, edges, triangular faces, etc.) closed under intersections, which compared to generic hypergraphs have favorable algebraic properties and deep connections to algebraic topology that can be exploited for network analysis. For instance, SCs are naturally endowed with higher-order Laplacian operators (so called Hodge-Laplacians) — extensions of the well-known graph Laplacian that is pivotal for network analysis — which can be used to reveal additional information about the system under investigation.
Recovering network structure from data
We have studied the problem of recovering the topology of a graph (or coarser features of it, such as communities) from observing snapshots of multiple independent network processes. For instance, we observe the opinion profiles of a group of agents for a set of independent topics and our goal is to recover the precise relationships between the agents (or detect communities), as specified by the unknown social network underlying the exchange of opinions. A key realization is that the covariance structure of the outputs of the observed network process contain essential information about the graph that we are trying to recover. Hence, we leverage concepts from spectral graph theory and convex optimization to unveil the underlying network structure.
- H. T. Wai, S. Segarra, A. E. Ozdaglar, A. Scaglione and A. Jadbabaie, Community Detection from Low-rank Excitations of Graph Filters, IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, Canada, April 15-20, 2018. Best Student Paper Award.
- S. Segarra, M. T. Schaub and A. Jadbabaie, Network Inference from Consensus Dynamics, IEEE Conference on Decision and Control, pp. 3212-3217, Melbourne, Australia, December 12-15, 2017.
- Soheil Feizi, Gerald Quon, Mariana Mendoza, Muriel Medard, Manolis Kellis, Ali Jadbabaie. Spectral Alignment of Graphs, IEEE Transactions on Network Science and Engineering, accepted, August2018. [code]